Задача №: 27141. Прототип №: 27141
Площадь поверхности куба равна 24. Найдите его объем.

Ответ:
Показать/скрыть правильный ответ

Задача №: 27148. Прототип №: 27148
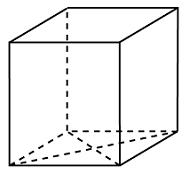
В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.

Ответ:
Показать/скрыть правильный ответ

Задача №: 27151. Прототип №: 27151
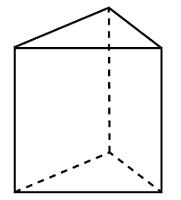
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

Ответ:
Показать/скрыть правильный ответ

Задача №: 27153. Прототип №: 27153
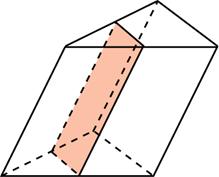
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

Ответ:
Показать/скрыть правильный ответ

Задача №: 27157. Прототип №: 27157
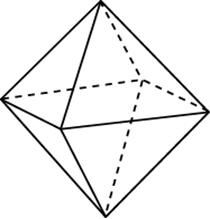
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

Ответ:
Показать/скрыть правильный ответ

Задача №: 27158. Прототип №: 27158
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

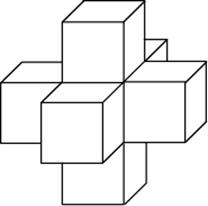
Ответ:
Показать/скрыть правильный ответ

Задача №: 27161. Прототип №: 27161
Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

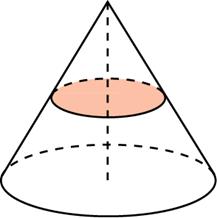
Ответ:
Показать/скрыть правильный ответ

Задача №: 27162. Прототип №: 27162
Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

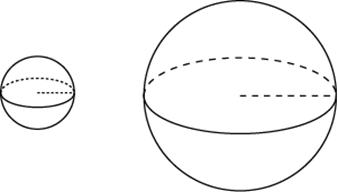
Ответ:
Показать/скрыть правильный ответ

Задача №: 27163. Прототип №: 27163
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

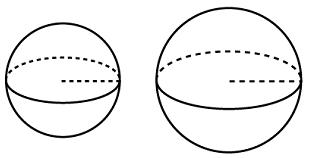
Ответ:
Показать/скрыть правильный ответ

Задача №: 27168. Прототип №: 27168
Объём первого куба в 8 раз больше объёма второго куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Ответ:
Показать/скрыть правильный ответ