Элементы 21—30 из 51.
Задача №:
317701.
Прототип №: 317540
На рисунке изображён график функции \(y=f(x)\) и десять точек на оси абсцисс: \(x_1\), \(x_2\), \(x_3\), \(\dots\), \(x_{10}\). В скольких из этих точек производная функции \(f(x)\) отрицательна?
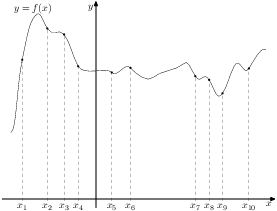
Ответ:

Правильный ответ: 7
Показать/скрыть правильный ответ
317684317686317688317690317692317694317696317698317700317702